A Taste of

Topological Data Analysis (TDA)

(Shape Reconstruction)

Dr. Sushovan Majhi
School of Information, UCB
September 30, 2021

Good afternoon, everyone. I would like to first thank Vincent for the invitation and the Applied Math group at Hunter for hosting the HCAM seminar series. It's a great initiative.
I go by Sush. I am fresh graduate from Tulane University, New Orleans; Currently a postdoc at the School of Information, UC Berkeley.
To get a copy of my slides online, please scan the QR code or go to 'smajhi.com/21-fa-hunter' using your browser.
I have tried to make the ride today as gentle as possible for the audience. To better cusion it, I will try use a lot of pictures and visualization tools -- sparing you of all the bells and whistles and the mathematical proofs. Although, an interested audience is welcome to call on our papers online. I will put the pointers at some point.
Alright --- without further adieu, let's get started.

Collaborators

Alongside instructing statistics at UCB, I have been continuing my research broadly in data science. Although I take a keen interest in questions arising in topological data analysis, computational topology and computational geometry, I always keep an eye out for practical problems where I can test my topological hammer.

I have had the opportunity to work with some very nice mathematicians, computer scientists, and physicists. In the top-left corner, is my PhD adviser Carola Wenk. She is the chair of computer science at Tulane.

Carola Wenk
Tulane University
(PhD adviser)

Brittany Fasy
Montana State U

Jeff Vitter,
U of Mississippi

Md. Nurujjaman
National Institute of Technology
India

Erin Chambers
St. Louis University

Liz Munch
Michigan State U

The Manifesto

Introduction to TDA
The Reconstruction Problem
Vietoris-Rips Complex
A Possible Solution
Opportunities in TDA
Questions

Topological Data Analysis (TDA)

In 2015, as a young graduate student when I was on the hunt for good projects, I was drawn in by the application of topology and geometry in data science. Still in its cradle at the time, TDA could attract only a few hundred researchers in the states and could afford only one or two major conferences and workshops around the year.
Topology, after all, is a branch of geometry---it is the systematic study of similarity of abstract shapes, or topological spaces through various invariants, like homology groups, cohomology rings, homotopy groups, and so on.
It's difficult to say how or when TDA started to take shape, but in the early years of the first decade of the century, computer scientists showed an interest to algorithmcally compute those topological invariants. The domain is now called Computational Topology.

Around the same time, there was an effort to employ topological ideas to solve practical problems, e.g., ...
Emboldened by the success of computational and applied topology in providing tanable solutions to practical problems, the TDA community emerged to bestow a topological toolkit on the realm of data science.
It straddles between computational topology and applied topology affording methods inspired by a fair count of ideas from both topology, geometry, and computer science. TDA now is growing apace, it is a field no longer esoteric to applied mathematicians, a name not so unheard of in the mainstream data science. Business ventures like Ayasdi even took it to the silicony valley.

Computational Topology
> algorithmcally compute various topological invariants, e.g., homology groups, Betti numbers, Euler characteristic, etc
Applied Topology
> apply topological ideas in sensor network, motion planning in robotics, configuration spaces etc
TDA
> learning from big data, (stratified) manifold learning, shape reconstruction and comparison, and so much more...

Shape Reconstruction

Shapes

Smooth Manifolds (the good ones)

However, more often than not, practical applications deal with shapes that are far from being a smooth manifold. The map of the neighborhood of Hunter can be modelled as a graph, where the intersections are thought of as the vertices, whereas the roads the edges.
Clearly, a graph is NOT a manifold -- because of the branchings at the intersections and the corners.
As our story unfolds, we will see that our reconstruction results can handle smooth manifolds also graphs -- as well as more sophisticated and general class of shapes -- which we call geodesic spaces.

Our shapes of interest (the ugly ones)

Geodesic Spaces

So, we first get the definition straight.
In geometry, a geodesic mimics the concept of SHORTEST PATH between two points on a graph.
Explain the picture.
Define geodesic spaces
It is evident from the definition that a graph is a geodesic space, so is the road-network around Hunter. Also any compact, sub-manifold of the Euclidean space is a geodesic space. Higher dimensional simplicial complexes are also examples of geodesic spaces.
For the curious audience, the sphere -- if punctured at a point -- no longer remains a geodesic space.

For any two points $x,y\in X\subseteq\mathbb{R}^N$, there exists a geodesic or shortest path.

For a geodesic space $X\subseteq\mathbb{R}^N$, the distortion $$\delta=\sup_{x\neq y}\frac{\color{red}{d_L(x,y)}}{\color{blue}{\|x-y\|}}.$$
For a geodesic space $X\subseteq\mathbb{R}^N$, the convexity radius $\rho$ is the half of the (ant) distance between a pair of furthest points $x,y\in X$ that have a unique geodesic. For a unit length circle, its convexity radius is one quarter.

The Reconstruction Problem

Noisy Sample (www.smajhi.com/shape-reconstruction)

Sample from $S^1\vee S^1$ (www.smajhi.com/shape-reconstruction)

GPS Traces Berlin (www.mapconstruction.org)

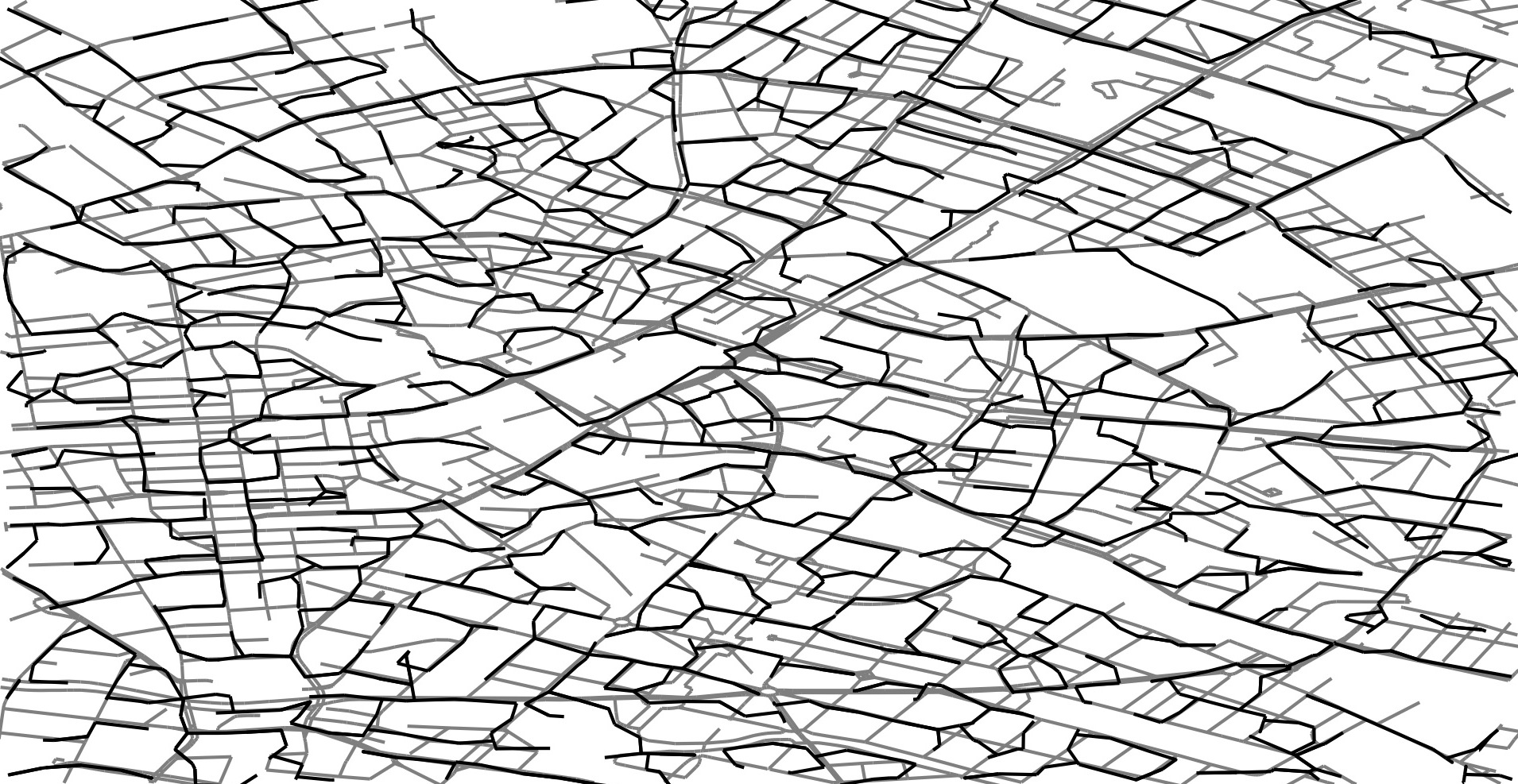
Reconstructed Map or Road-Network (www.mapconstruction.org)

Problem Statement

Let $X$ be a hidden geodesic subset of $\mathbb{R}^N$
We have a sample or a point-cloud $(S,\|\cdot\|)$
$S$ is reasonably dense around $X$.

Q: Can we infer the toplogy of $X$ from $S$? What does inference even mean in such a reconstruction context?

Compute $H_*(X)$ and/or $\pi_*(X,b)$ from $S$
Construct $\widetilde{X}$ homotopy equivalent to $X$
$\widetilde{X}$ has a geometrically-close embedding in $\mathbb{R}^N$

Density via Hausdorff Distance

Hausdorff distance $d_H(A,B)$ is
$\max\{$ $a$, $b$ $\}=$ $b$

💡

If $d_H(A,B) <\varepsilon$, then
> each point $a\in A$ has a point $b\in B$ with $||a-b|| <\varepsilon$, and
> each point $b\in B$ has a point $a\in A$ with $||a-b|| <\varepsilon$.

Now as we have laid out the density conditions for a good sample in terms of Hausdorff distance, let's try to find a reconstruction. Our sample S is discrete set of points with the mutual distances defined on them. S does not have a rich topology! Currently, it can only have the discrete topology. In order to create a space \tilde X that we can call a reconstruction, we use the Vietoris-Rips complexes. Vietoris-Rips complexes were somewhat well-studied. However, the TDA community has extended its popularity beyond the limits of classical topology.

Vietoris-Rips Complex

For a metric space $(M,d_M)$ and scale $\varepsilon>0$, each subset $A$ of size $k$ with $diam_d(A)\leq\epsilon$ is a $(k-1)$-simplex of the Vietoris-Rips complex $VR_\varepsilon(M)$.

Let $X$ be a smooth sub-manifold. If $\epsilon>0$ is small and $d_H(X,S)$ is also small, then the Vietoris-Rips complex $VR_\varepsilon(S)$ is homotopy equivalent to $X$.

Geodesic Spaces

small $\epsilon$ + dense sample trick
does not work
😢

Our Approach

$X\subseteq\mathbb{R}^N$ is a geodesic subspace $(X,d_L)$
Distortion $\delta$ is finite
Convexity radius $\rho$ is positive
$d_H(X,S)$ is small

Topological Reconstruction

If $d_H(X,S) <\epsilon<\frac{\rho}{2\delta(3\delta+1)}$, the image $$Im(j_*)\simeq\pi_*(X),$$ where $j:\mathcal{VR}_{\epsilon}(S)\to\mathcal{R}_{\frac{1}{2}(3\delta+1)\epsilon}(S)$.

Geometric Reconstruction

If $d_H(G,S) <\epsilon<\frac{\rho}{2\delta(3\delta+1)}$, we can output $\widetilde{X}$ such that $$\widetilde{X}\simeq G,$$ and $d_H(G,\widetilde{X})$ is small.

Remarks on Reconstruction

Our geometric reconstruction works for planar graphs. Spatial graphs? My very recent work!
Geometric reconstruction of higher-dimensional objects, like embedded simplicial complexes.
Incorporate statistical treatments.
The visualization tool is available as a webapp (github.com/sushovan4/shape-reconstruction). Need volunteers to extend it.

Opportunities

Companies like Ayasdi are hiring topological data scientists and interns
Open-source projects in TDA: Gudhi (C++), Scikit-tda (Python), tdajs (Typescript/JS)
Graduate schools like OSU, Michigan S, Duke, Montana State, Tulane have TDA grants/projects
I also have some cool problems and projects (theory and application)
smajhi@berkeley.edu

References

Adams_2019
fasy2018reconstruction
fw17

The speaker will now accept
QUESTIONS.

Topological Data Analysis (TDA)

(Shape Reconstruction)

Collaborators

The Manifesto

Topological Data Analysis (TDA)

Shape Reconstruction

Shapes

Geodesic Spaces

The Reconstruction Problem

Problem Statement

Density via Hausdorff Distance

Vietoris-Rips Complex

Geodesic Spaces

Our Approach

Topological Reconstruction

Geometric Reconstruction

Remarks on Reconstruction

Opportunities

References

🤔